| Lesson 4 | Convert Decimal to Binary |
| Objective | Convert numbers between decimal and binary |
Algorithm for converting a Decimal Number to its Binary Equivalent
The algorithm to convert a decimal number to its binary equivalent is based on the process of successive division by 2, where you keep track of the remainders at each step. Here is a step-by-step description of the algorithm:
Here is the algorithm in a more formal representation:
In this algorithm, the `//` operator represents integer division, which means you divide and then floor the result to get an integer. The `%` operator is the modulo operation that gives you the remainder. Prepending each remainder to the binaryNumber ensures that you are building the binary number from the least significant bit to the most significant bit.
To illustrate with an example, let’s convert the decimal number `13` to binary:
Now, take the remainders in reverse order to get 1101, which is the binary equivalent of the decimal number 13.
- Initialize: Start with the decimal number that you wish to convert to binary.
- Divide the Number by 2: Divide the decimal number by 2.
- Record the Remainder: After the division, record the remainder. It will be either 0 or 1.
- Update the Quotient: Replace the original number with the quotient obtained from the division.
- Repeat the Process: Repeat the division by 2 with the new quotient, recording the remainder each time.
- Continue Until the Quotient is 0: Continue the process of dividing by 2 and recording the remainder until the quotient becomes 0.
- Collect the Remainders: The binary representation consists of the remainders you have recorded, taken in reverse order (i.e., the remainder from the last division is the most significant bit).
Here is the algorithm in a more formal representation:
function convertDecimalToBinary(decimalNumber)
binaryNumber = empty list or string
while decimalNumber > 0
remainder = decimalNumber % 2
prepend remainder to binaryNumber
decimalNumber = decimalNumber // 2 (use integer division)
end while
return binaryNumber
end function
In this algorithm, the `//` operator represents integer division, which means you divide and then floor the result to get an integer. The `%` operator is the modulo operation that gives you the remainder. Prepending each remainder to the binaryNumber ensures that you are building the binary number from the least significant bit to the most significant bit.
To illustrate with an example, let’s convert the decimal number `13` to binary:
- 13 / 2 = 6 with a remainder of 1.
- 6 / 2 = 3 with a remainder of 0.
- 3 / 2 = 1 with a remainder of 1.
- 1 / 2 = 0 with a remainder of 1.
Now, take the remainders in reverse order to get 1101, which is the binary equivalent of the decimal number 13.
Converting a decimal number to its binary equivalent is a little more challenging.
Here's one approach.
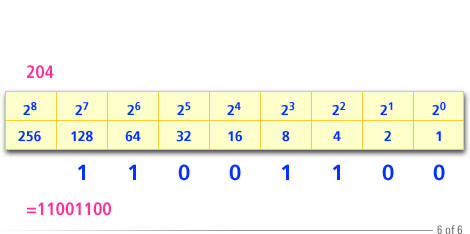
The following series of images describe how to convert the decimal number 204 to binary.
- Find the highest power of 2 less than or equal to the decimal number. In your binary number, place a 1 in the position corresponding to this power of 2.
- Subtract the power of 2 found in step 1 from the decimal number to obtain a new decimal number. If the new decimal number is 0, then you are done; otherwise, return to step 1 with the new decimal number.
The following series of images describe how to convert the decimal number 204 to binary.
Converting from decimal to binary

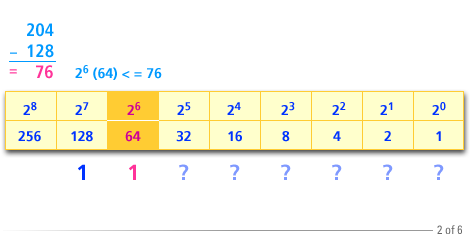
Thus the binary number should have a 1 in the position corresponding to 2^6.
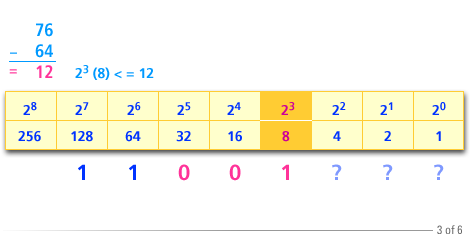
Thus the binary number should have a 1 in the position corresponding to 2^3.
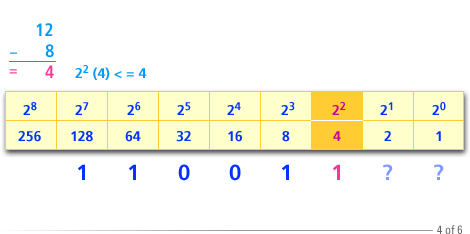
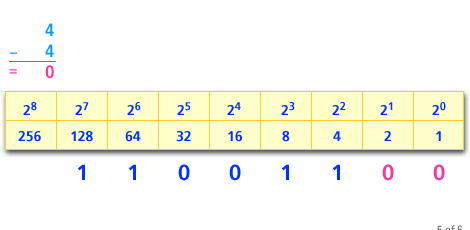
Computer Science Structured Approach
- The largest power of 2 less than or equal to 204 is 2 raised to the 7th = 128.
- Subtracting 128 from 204 gives 76. The largest power of 2 less than or equal to 76 is 2 raised to the 6th = 64.
- Subtracting 64 from 76 gives 12. The largest power of 2 less than or equal to 12 is 2 raised to the 3 = 8.
- Subtracting 8 from 12 gives 4. The largest power of 2 less than or equal to 4 is 2^2 =4.
- Subtracting 4 from 4 givess 0. We are completed.
- From our work we see that the binary equivalent of 204 should have 1s in the corresponding to 2^7, 2^6, 2^3 and 2^2.
Binary numbers can require many digits. In the next lesson, you will look at how binary numbers can be expressed more compactly using hexadecimal form.
Converting Binary Numbers - Quiz
Click the Quiz link below to see how well you understand binary numbers.
Converting Binary Numbers - Quiz
Converting Binary Numbers - Quiz